LASSO, mis on lühend kõige vähem absoluutse kokkutõmbumise ja valikuoperaatorist, on statistiline valem, mille peamine eesmärk on tunnuste valik ja andmemudelite seadistamine. Meetodi tutvustas esmakordselt 1996. aastal statistikaprofessor Robert Tibshirani. LASSO tutvustab mudeli summale parameetreid, andes sellele ülemise piiri, mis toimib piiranguna sellele, et summa hõlmaks absoluutseid parameetreid lubatud vahemikus.
LASSO meetod seadistab mudeli parameetrid regressioonikoefitsientide kokkutõmbamise abil, vähendades mõned neist nulli. Funktsioonide valimise faas toimub pärast kahanemist, kus mudelis valitakse iga nullist erinev väärtus. See meetod on oluline statistiliste mudelite puhul levinud ennustusvigade minimeerimisel. Kvantitatiivne analüüs Kvantitatiivne analüüs on mõõdetavate ja kontrollitavate andmete, nagu tulud, turuosa ja palgad, kogumise ja hindamise protsess, et mõista toote käitumist ja tulemuslikkust. äri. Andmetehnoloogia ajastul peetakse kvantitatiivset analüüsi eelistatud lähenemiseks teadlike otsuste langetamisel. .
LASSO pakub kõrge ennustustäpsusega mudeleid. Täpsus suureneb, kuna meetod hõlmab koefitsientide kahanemist, mis vastutasuks vähendab dispersiooni ja minimeerib eelarvamusi. See toimib kõige paremini siis, kui vaatlusi on vähe ja funktsioonide arv on suur. See tugineb suuresti parameetrile λ, mis on kahanemise juhtiv tegur. Mida suuremaks muutub λ, siis sunnitakse rohkem koefitsiente olema null.
Kui λ on võrdne nulliga, saab mudel tavalise väikseimate ruutude regressiooniks. Järelikult, kui λ suureneb, väheneb dispersioon märkimisväärselt ja suureneb ka tulemuse kallutatus. Lasso on ka kasulik tööriist kõigi muutujate kõrvaldamiseks, mis pole asjakohased ja mis pole seotud muutujaga.
LASSO statistilistes lineaarsetes mudelites
Statistiline mudel on probleemi tegelik matemaatiline esitus. Mudel peaks väljendama probleemi võimalikult lähedal reaalsele maailmale, muutes selle samal ajal lihtsaks ja arusaadavaks. Mudel koosneb selgitavatest ja reageerivatest muutujatest.
The selgitav muutuja on sõltumatu muutuja, mis jääb uurija otsustada. Sõltumatud muutujad on mudeli sisendid, mida teadlane saab mõõta, et teha kindlaks nende mõju mudeli tulemustele.
The vastuse muutuja on sõltuv muutuja Sõltuv muutuja Sõltuv muutuja on see, mis muutub sõltuvalt teise muutuja väärtusest, mida nimetatakse sõltumatuks muutujaks. mis moodustab katse põhirõhu. See moodustab katse tulemuse, mis võib ühemõõtmeliste mudelite korral olla üks tulemus või mitmemõõtmeliste mudelite korral mitme tulemus.
LASSO moodustab mudeli loomise protsessi lahutamatu osa, eriti funktsioonide valiku abil. Funktsioonide valimise etapp aitab valida selgitavaid muutujaid, milleks on sõltumatud muutujad ja seega ka mudeli sisestatud muutujad.
Sisendmuutujad on olulised elemendid, mis määravad mudeli väljundi ja aitavad mõõta nende mõju reaktsioonimuutujatele. Õigete muutujate valimine määrab mudeli täpsuse. LASSO funktsioonide valimise etapp aitab muutujaid õigesti valida.
Hinnang LASSO-ga
Statistilised mudelid tuginevad muutujate täpseks valimiseks ja seadistamiseks LASSO-le. Lineaarse regressiooni regressioonanalüüs Regressioonanalüüs on statistiliste meetodite kogum, mida kasutatakse sõltuva muutuja ja ühe või mitme sõltumatu muutuja vaheliste seoste hindamiseks. Seda saab kasutada muutujate seose tugevuse hindamiseks ja nende vahelise tulevase suhte modelleerimiseks. näiteks kehtestab LASSO ruutude summa ülemise piiri, minimeerides seega mudelis esinevaid vigu. LASSO hindaja sõltub parameetrist λ.
Parameeter λ kontrollib kokkutõmbumise tugevust, kus λ suurenemine põhjustab kokkutõmbumise kasvu. Kõigi koefitsientide summa ülemine piir on pöördvõrdeline parameetriga λ. Kui ülemise piiri väärtus suureneb, väheneb parameeter λ. Kui ülemine piir väheneb, suureneb parameeter λ samaaegselt.
Kui ülemine piir tõuseb lõpmatuse suunas, läheneb parameeter λ nullile, teisendades seega katse tavaliseks kõige väiksemaks ruuduks, kus parameeter λ on alati võrdne nulliga. Kui ülemine piirkoefitsient läheneb nullile, suureneb parameetri λ väärtus lõpmatuse suunas.
LASSO geomeetria
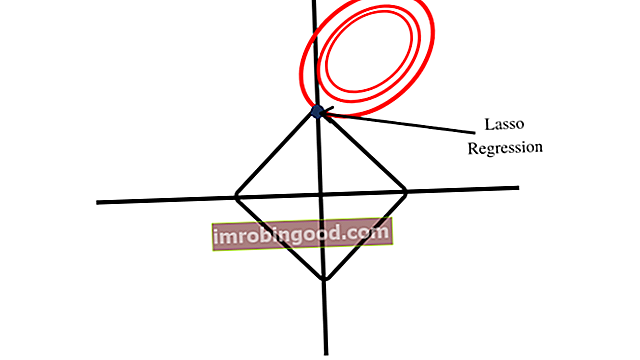
LASSO moodustab joonisel oma piirangupiirkonna jaoks teemandi kuju, nagu on näidatud alloleval pildil. Rombikujuline kuju sisaldab nurki, erinevalt harja taandumisest moodustunud ümmargusest kujust. Esimese punkti lähedus nurgale näitab, et mudelil on üks koefitsient, mis on võrdne nulliga.
Ridge regressioonipiirangute piirkond moodustab ümmarguse kuju, mis ei sisalda nurki, mis on sarnane LASSO piirangute piirkonna kujundamisel. Ridge regressioonikordajad ei saa seetõttu olla võrdsed nulliga.
Kaalutud LASSO
Kaalutud LASSO on teadlase tulemus, mis karistab regressioonikordajaid eraldi. See tähendab, et selle asemel, et karistada kõigi koefitsientide ühist parameetrit λ, karistatakse koefitsiente individuaalselt, kasutades erinevaid parameetreid.
Kaalu saab määrata LASSO algoritmi abil, et määrata kaalud täpseks modelleerimiseks. Regressioonikordajate sarnane kaal on ühistu LASSO, kus koefitsiente karistatakse rühmades, mida peetakse sarnaseks.
Lisaressursid
Finance on sertifitseeritud pangandus- ja krediidianalüütiku (CBCA) ™ CBCA ™ sertifikaadi ametlik pakkuja. Certified Banking & Credit Analyst (CBCA) ™ akrediteerimine on krediidianalüütikute ülemaailmne standard, mis hõlmab finantseerimist, raamatupidamist, krediidianalüüsi, rahavoogude analüüsi, pakti modelleerimine, laenu tagasimaksed ja palju muud. sertifitseerimisprogramm, mille eesmärk on muuta keegi maailmatasemel finantsanalüütikuks.
Finantsanalüüsi alal õppimiseks ja teadmiste arendamiseks soovitame tungivalt allpool olevaid täiendavaid finantsressursse:
- Prognoosimeetodid Prognoosimeetodid Parimad prognoosimeetodid. Selles artiklis selgitame nelja tüüpi tulude prognoosimise meetodeid, mida finantsanalüütikud kasutavad tulevaste tulude prognoosimiseks.
- Sõltumatu muutuja Sõltumatu muutuja Sõltumatu muutuja on sisend, eeldus või draiver, mida muudetakse, et hinnata selle mõju sõltuvale muutujale (tulemusele).
- Mitu lineaarset regressiooni Mitu lineaarset regressiooni Mitu lineaarset regressiooni osutab statistilisele tehnikale, mida kasutatakse sõltuvate muutujate väärtuse põhjal sõltuva muutuja tulemuse ennustamiseks
- Stsenaariumide analüüs Stsenaariumide analüüs Stsenaariumide analüüs on meetod, mida kasutatakse otsuste analüüsimiseks spekuleerides finantsvõimaluste mitmesuguseid võimalikke tulemusi. Finantsmudelites on see

