Juhuslik mets on ennustuste ja käitumise analüüsi modelleerimisel kasutatav tehnika, mis on üles ehitatud otsustuspuudele. See sisaldab palju otsustuspuid, mis esindavad juhusliku metsa sisestatud andmete klassifitseerimise selget eksemplari. Juhuslik metsatehnika võtab juhtumeid individuaalselt arvesse, võttes valitud prognoosiks selle, kellel on enamus häältest.
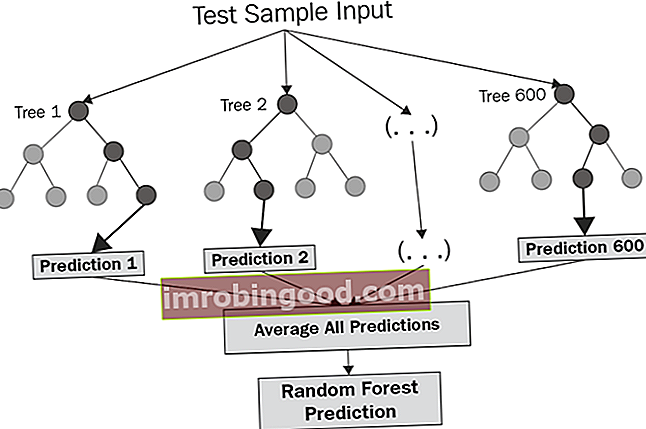Joonis 1. Juhuslik metsaehitus (allikas)
Iga klassifikatsioonipuu võtab lähteandmekogumi proovidest sisendi. Seejärel valitakse juhuslikult funktsioonid, mida kasutatakse puu kasvatamiseks igas sõlmes. Iga metsa puud ei tohiks kärpida enne harjutuse lõppu, kui ennustus on otsustavalt saavutatud. Sel viisil võimaldab juhuslik mets kõikidel nõrkade korrelatsioonidega klassifikaatoritel luua tugeva klassifikaatori.
Kiire kokkuvõte
- Juhuslik mets on otsustuspuude kombinatsioon, mida saab modelleerida ennustamiseks ja käitumise analüüsimiseks.
- Metsas asuvat otsustuspuud ei saa proovide võtmise ja seega ka prognoosivaliku jaoks kärpida.
- Juhusliku metsa tehnika saab hakkama suurte andmekogumitega, kuna see on võimeline töötama paljude tuhandeteni ulatuvate muutujatega.
Ennustuste modelleerimine
Juhusliku metsa meetodiga saab ehitada ennustusmudeleid, kasutades juhuslikke metsa regressioonipuid, mis on tavaliselt tugevate ennustuste saamiseks kärpimata. Regressioonipuudel kasutatakse bootstrapi proovivõtumeetodit, mida ei tohiks kärpida. Optimaalsete jagamisfunktsioonide moodustamiseks võetakse optimaalsed sõlmed puu kogu sõlmedest.
Optimaalse jagamisfunktsiooni valimisel kasutatud juhuvalimi meetod vähendab korrelatsiooni ja seega ka regressioonipuude dispersiooni. See parandab metsas olevate puude ennustamisvõimet. Bootstrapi abil proovide võtmine suurendab ka üksikute puude iseseisvust.
Muutuv tähtsus
Muutujad (tunnused) on juhusliku metsa jaoks olulised, kuna mudelite tõlgendamine, eriti bioloogilisest vaatenurgast, on väljakutse. Naiivne lähenemisviis näitab muutujate olulisust, omistades muutujale olulisuse selle põhjal, kui palju on need puud valimisse kaasatud. Seda saab hõlpsasti saavutada, kuid see on väljakutse, kuna mõju kulude vähendamisele ja täpsuse suurenemisele on üleliigne.
Permutatsiooni tähtsus on mõõt, mis jälgib ennustuse täpsust, kus muutujad juhuslikult permutatakse kotist väljas olevate proovide põhjal. Permutatsiooni olulisuse lähenemine töötab paremini kui naiivne lähenemine, kuid kipub olema kallim.
Kuna juhusliku metsa väljakutsed ei suuda ennustusi bioloogilisest vaatenurgast piisavalt hästi tõlgendada, tugineb tehnika naiivsele, keskmisele lisandite vähenemisele ja permutatsiooni olulisuse lähenemisviisidele, et anda neile väljakutsetele otsene tõlgendatavus. Need kolm lähenemist toetavad mitme kategooriaga ennustajaid.
Sarnase kategooriate arvuga pidevate ennustajate muutujate puhul ei ilmne nii permutatsiooni olulisuse kui ka keskmise lisandite vähenemise lähenemisviiside puhul eelarvamusi Andmekaevandamise eelarvamused Andmekaevandamise eelarvamused viitavad eeldusele, kui oluline on kaupleja sündmusele omistatud turul, mis tegelikult oli juhuse või ettenägematu tulemus. Muutuva valikuga kaasneb sageli erapoolikus. Selle vältimiseks tuleks läbi viia alavõtmine ilma asendamiseta ja kui kasutatakse tingimuslikku järeldust, tuleks kasutada juhuslikku metsatehnikat.
Kaldus juhuslikud metsad
Kaldus juhuslikud metsad on ainulaadsed selle poolest, et nad kasutavad sõlmedes tavapäraste otsalõikude asemel otsustamiseks kaldus lõhesid. Kaldus metsad näitavad palju paremust, näidates järgmisi omadusi.
Esiteks saavad nad eraldada jaotused koordinaattelgedel ühe mitmemõõtmelise jaotuse abil, mis hõlmaks tavapäraselt vajalikke sügavate telgedega joondatud jaotusi. Teiseks võimaldavad need kavandatud piirangute osas langetada otsustamispuude eelarvamusi. Tavalised teljega joondatud jaotused vajavad sarnaste klasside eraldamisel kaldus jaotustega veel kahte pesitsustaset, mis muudab selle kasutamise lihtsamaks ja tõhusamaks.
Juhuslik metsaklassifikaator
Juhusliku metsa klassifikaator on ennustuspuude kogum, kus iga puu sõltub juhuslikult valitud vektoritest, mis on valimisse võetud iseseisvalt, sarnase jaotusega kõigi teiste juhusliku metsa puudega. Algselt masinõppeks mõeldud klassifikaator on populaarsust kogunud kaugseire kogukonnas, kus seda kasutatakse suure täpsuse tõttu kaugseirega kujutiste klassifikatsioonis. Samuti saavutatakse protsessis vajalik nõuetekohane kiirus ja tõhus parameetrite määramine. Juhuslik metsa klassifikaator käivitab juhuslikud valimid, kus valitakse kõigi puude suurima häältega ennustus.
Puude individuaalsus on oluline kogu protsessi vältel. Iga puu individuaalsus on tagatud järgmiste omaduste tõttu. Esiteks kasutab iga valimis olev puu treening algsete treeningvalimite juhuslikke alamhulki. Teiseks valitakse optimaalne poolitus lõikamata puusõlmede juhuslikult valitud tunnuste hulgast. Kolmandaks, iga puu kasvab piirideta ja seda ei tohiks üldse kärpida.
Juhuslike metsade eelised
Juhuslikud metsad esitavad hinnanguid erineva tähtsusega, s.t närvivõrkude kohta. Need pakuvad ka parimat meetodit puuduvate andmetega töötamiseks. Puuduvad väärtused asendatakse muutujaga, mis ilmub konkreetses sõlmes kõige rohkem. Kõigi saadaolevate klassifitseerimismeetodite hulgas on juhuslikud metsad kõige täpsemad.
Juhusliku metsatehnikaga saab hakkama ka suurte andmetega, mille arv on tuhandeid. See suudab andmekogumeid automaatselt tasakaalustada, kui klass on teistes andmetes olevatest klassidest haruldasem. Samuti käsitleb meetod muutujaid kiiresti, muutes selle keerukate ülesannete jaoks sobivaks.
Rohkem ressursse
Finance pakub finantsmodelleerimise ja hindamise analüütikule (FMVA) ™ FMVA® sertifikaati. Liituge 350 600+ üliõpilasega, kes töötavad sellistes ettevõtetes nagu Amazon, JP Morgan ja Ferrari sertifitseerimisprogrammis neile, kes soovivad oma karjääri järgmisele tasemele viia. Oma teadmistebaasi õppimise ja arendamise jätkamiseks uurige palun allpool olevaid täiendavaid asjakohaseid finantsressursse:
- Ristlõikeandmete analüüs Ristlõikeandmete analüüs Ristlõikeandmete analüüs on ristlõikeandmekogumite analüüs. Uuringud ja valitsuse andmed on läbilõikeandmete levinumad allikad
- Klastrite valimine Klastrite valimine Statistikas on klastrivalim valimi moodustamise meetod, mille käigus kogu uuringu populatsioon jaguneb väliselt homogeenseteks, kuid sisemiselt
- Normaalne jaotus Normaalne jaotus Normaalset jaotust nimetatakse ka Gaussi või Gaussi jaotuseks. Seda tüüpi levitamist kasutatakse laialdaselt loodus- ja sotsiaalteadustes. The
- Roy ohutuse esimene kriteerium Roy ohutuse esimene kriteerium Roy ohutuse esimene kriteerium on riskijuhtimistehnika, mida investorid kasutavad portfelli võrdlemiseks ja valimiseks kriteeriumi alusel, et tõenäosus
