Elastne lineaarne regressioon kasutab regressioonimudelite seadustamiseks nii lasso- kui ka ridge-meetodite karistusi. Tehnika ühendab nii lasso LASSO LASSO, mis on lühend lühimast absoluutse kokkutõmbumise ja valikuoperaatorist, on statistiline valem, mille põhieesmärk on funktsioonide valimine ja seadistamine ning harja regressioonimeetodid, õppides nende puudustest statistiliste mudelite seadistamise parandamiseks.
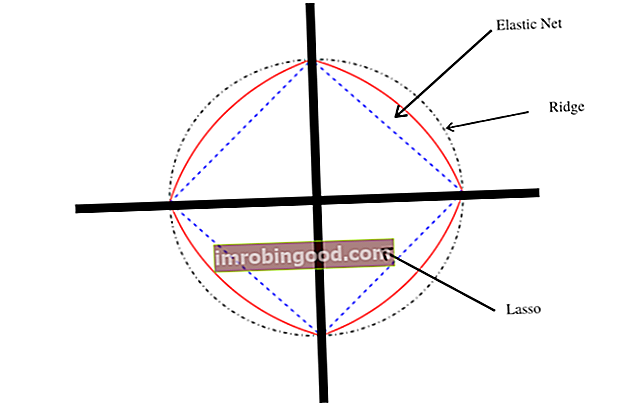
Elastse võrgu meetod parandab lasso piiranguid, st kui lasso võtab mõne mõõtmega andmete saamiseks paar proovi, võimaldab elastse võrgu protseduur hõlmata muutujate arvu kuni küllastumiseni. Juhul, kui muutujad on omavahel tihedalt seotud rühmad, valib lasso selliste rühmade hulgast ühe muutuja ja ignoreerib ülejäänud täielikult.
Lasso leitud piirangute kõrvaldamiseks sisaldab elastne võrk trahvis ruutulavastust (|| β || 2), mis eraldiseisvalt muutub harja regressiooniks. Karistuse ruutulatus tõstab kaotuse funktsiooni kumeruse poole. Elastne võrk tugineb mõlema maailma parimatele - st lasso ja harja regressioonile.
Elastse võrgu meetodi hinnangu leidmise protseduuris on kaks etappi, mis hõlmavad nii lasso- kui ka regressioonimeetodeid. Kõigepealt leiab see harja regressioonikordajad ja viib seejärel läbi teise sammu, kasutades koefitsientide lasso tüüpi kahanemist.
Seetõttu jagatakse selle meetodi korral koefitsiendid kahte tüüpi kahanemisteks. Elastse võrgu naiivse versiooni kahekordne kokkutõmbumine põhjustab prognoositavuse madalat efektiivsust ja suurt kallutatust. Selliste efektide korrigeerimiseks suurendatakse koefitsiente, korrutades need (1 + λ2).
Kiire kokkuvõte
- Elastse võrgu meetod teostab muutuja valimist ja seadistamist üheaegselt.
- Elastse võrgu tehnika on kõige sobivam, kui mõõtmete andmed on suuremad kui kasutatud proovide arv.
- Rühmituste ja muutujate valik on elastse võrgu tehnika võtmeroll.
Elastne võrgu geomeetria
Dekarteesia tasapinnale joonisel langeb elastne võrk harja ja lasso regressioonitükkide vahele, kuna see on nende kahe regressioonimeetodi kombinatsioon. Elastse võrgu joonisel on tippudes ka singulaarsus, mis on hõreduse jaoks oluline. Sellel on ka ranged kumerad servad, kus kumerus sõltub α väärtusest.
Kumerus sõltub ka korrelatsioonist sõltuvast rühmitamisefektist Korrelatsioon Korrelatsioon on kahe muutuja vahelise seose statistiline mõõde. Mõõtu saab kõige paremini kasutada muutujate vahel, mis näitavad omavahel lineaarset suhet. Andmete sobivust saab visuaalselt kujutada hajusdiagrammil. valitud muutujatest. Mida suurem on muutujate korrelatsioon, seda suurem on rühmitusefekt ja seega ka suurem valimisse kuuluvate muutujate arv.
Muutujate valik
Mudeli loomine eeldab muutujate valimist, et moodustada ennustajate alamhulk. Elastne võrk kasutab probleemilähenemist p >> n, mis tähendab, et ennustajate arv on suurem kui mudelis kasutatud proovide arv. Elastne võrk on asjakohane, kui muutujad moodustavad rühmad, mis sisaldavad väga korreleeritud sõltumatuid muutujaid Sõltumatu muutuja Sõltumatu muutuja on sisend, eeldus või draiver, mida muudetakse, et hinnata selle mõju sõltuvale muutujale (tulemusele). .
Täpsuse suurendamiseks on mudeli koostamise menetlusse kaasatud muutuv valik. Juhul, kui muutujate rühm on tugevalt seotud ja valimisse on valitud üks muutujatest, kaasatakse valimisse automaatselt kogu rühm.
CATREGi asutamine
CATREG on algoritm, mis hõlbustab muutujate teisendamist, nii lineaarseid kui mittelineaarseid. Algoritm kasutab muutujate teisendamisel kas mittemonotoonselt või monotoonselt mittelineaarsetes teisendustes sammu- ja spline-funktsioone. CATREG suudab muutujaid samaaegselt muundada ja seadistada mittemonotoonselt, ilma et oleks vaja tingimata esmalt laiendada muutujaid põhifunktsioonideks või näivmuutujateks.
Elastseid puhaskahjumi funktsioone võib nimetada ka tavalise väikseima ruudu regressioonikao funktsiooni piiratud tüübiks. CATREG-i algoritm on integreeritud elastsesse võrku, mis parandab saadud algoritmi efektiivsust ja lihtsust. Võrdluseks võib öelda, et elastne võrk ületab lasso, mis tõhususe ja lihtsuse poolest ületab ise harja regressiooni.
Elastne võrguregulatsioon
Reguleerimisprotseduuri ajal on l1 osa karistusest moodustab hõre mudeli. Teisalt teeb karistuse ruutjagu l1 osa stabiliseerumise teel stabiilsem, välistab valitud muutujate koguselimiidi ja soodustab grupeerimist.
Grupeerimisefekt aitab muutujaid korrelatsiooni abil hõlpsasti tuvastada. See täiustab proovivõtumenetlust. See suurendab ka valitud muutujate arvu, kuna kui ühest muutujast võetakse valim tugevalt korrelatsioonis rühmas, lisatakse valimisse automaatselt kõik selle rühma muutujad.
Tõhusad vabadusastmed
Efektiivsed vabadusastmed mõõdavad mudeli keerukust. Vabaduse astmed on olulised mudeli sobivuse hindamisel või täpsel ennustamisel. Vabadusastmed on kaasatud ka lineaarsete silendajate õppimisse. Mis tahes meetodiga, mis on seotud l1 karistus, tõstatab analüüsi väljakutse mudelite mittelineaarne olemus.
Elastset võrku saab kasutada ka muudes rakendustes, näiteks hõredas PCA-s, kus see saab põhikomponente, mida muudavad hõredad koormused. Teine rakendus on tuuma elastses võrgus, kus klassi tuumamasinate genereerimine toimub tugivektoritega.
Lisaressursid
Finance pakub sertifitseeritud pangandus- ja krediidianalüütiku (CBCA) ™ CBCA ™ sertifikaati. Sertifitseeritud pangandus- ja krediidianalüütiku (CBCA) ™ akrediteerimine on krediidianalüütikute globaalne standard, mis hõlmab finants-, raamatupidamis-, krediidianalüüsi, rahavoogude analüüsi, pakti modelleerimist, laenu tagasimaksed ja palju muud. sertifitseerimisprogramm neile, kes soovivad oma karjääri järgmisele tasemele viia. Oma teadmistebaasi õppimise ja arendamise jätkamiseks uurige palun allpool olevaid täiendavaid asjakohaseid finantsressursse:
- Otsustuspuu Otsuspuu Otsuspuu on puulaadse struktuuriga tugitööriist, mis modelleerib tõenäolisi tulemusi, ressursside maksumust, utiliite ja võimalikke tagajärgi.
- Sõltuv muutuja Sõltuv muutuja Sõltuv muutuja on see, mis muutub sõltuvalt teise muutuja väärtusest, mida nimetatakse sõltumatuks muutujaks.
- Mitu lineaarne regressioon Mitu lineaarne regressioon Mitu lineaarne regressioon viitab statistilisele tehnikale, mida kasutatakse sõltuvate muutujate väärtuse põhjal sõltuva muutuja tulemuse ennustamiseks
- Ülepaigaldamine Ületöötamine Ümberseadmine on statistikas kasutatav mõiste, mis viitab modelleerimisveale, mis ilmneb siis, kui funktsioon vastab liiga tihedalt konkreetsele andmekogumile