Kovariantsus - määratlus, valem ja praktiline näide

Matemaatikas ja statistikas Rahastamise põhistatistika mõisted Statistika kindel mõistmine on ülioluline, et aidata meil rahandust paremini mõista. Veelgi enam, statistikamõisted võivad aidata investoritel jälgida, kovariantsus on kahe juhusliku muutuja vahelise seose mõõdupuu. Mõõdikus hinnatakse, kui palju - mil määral - muutujad koos muutuvad. Teisisõnu on see sisuliselt kahe muutuja dispersiooni mõõt. Kuid mõõdikus ei hinnata muutujate sõltuvust.

Erinevalt korrelatsioonikordajast mõõdetakse kovariantsust ühikutes. Ühikud arvutatakse korrutades kahe muutuja ühikud. Dispersioon võib võtta mis tahes positiivseid või negatiivseid väärtusi. Väärtusi tõlgendatakse järgmiselt:

• Positiivne kovariantsus: Näitab, et kaks muutujat kipuvad liikuma samas suunas.
• Negatiivne kovariantsus: Näitab, et kaks muutujat kipuvad liikuma pöördsuundades.

Rahanduses Finance Finance'i finantsartiklid on loodud iseõppimise juhenditena, et õppida olulisi rahanduskontseptsioone veebis omas tempos. Sirvige sadu artikleid! , kasutatakse mõistet peamiselt portfelliteoorias. Üks selle levinumaid rakendusi portfelliteoorias on hajutamise mitmekesistamine Hajutamise mitmekesistamine on portfelliressursside või kapitali jaotamise meetod mitmesugustele investeeringutele. Hajutamise eesmärk on kahjude leevendamine, kasutades portfelli varade kovariantsust. Valides varad, millel puudub suur positiivne kovariantsus üksteisega, saab süsteemse riski osaliselt välistada.

Rahandus Matemaatika ettevõtte rahanduse kursusele uurib finantsmodelleerimiseks vajalikke finantsmatemaatika mõisteid. Mis on finantsmudelid Ettevõtte finantstulemuste prognoosimiseks tehakse finantsmudelid Excelis. Ülevaade sellest, mis on finantsmudelid, kuidas ja miks mudelit üles ehitada.

Kovariantsuse valem

Kovariantsivalem sarnaneb korrelatsioonivalemiga ja käsitleb andmepunktide arvutamist andmekogumi keskmisest väärtusest. Näiteks saab kahe juhusliku muutuja X ja Y kovariantsuse arvutada järgmise valemi abil (populatsiooni jaoks):

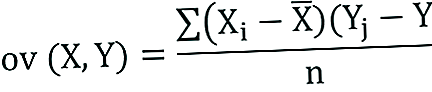
Kovariantsuse näidise jaoks on valemit veidi kohandatud:

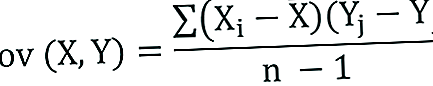
Kus:

• X_i - X-muutuja väärtused
• Y_j- muutuja Y väärtused
• X̄ - X-muutuja keskmine (keskmine)
• Ȳ - Y-muutuja keskmine (keskmine)
• n - andmepunktide arv

Kovariantsus ja korrelatsioon

Kovariantsus ja korrelatsioon hindavad mõlemad peamiselt muutujate suhet. Lähim analoog nende omavahelisele suhtele on dispersiooni ja standardhälbe suhe. Standardhälve Statistika seisukohalt on andmekogumi standardhälve mõõdetud sisalduvate vaatluste väärtuste vaheliste kõrvalekallete suuruse mõõt.

Kovariantsus mõõdab kahe juhusliku muutuja koguarvu variatsiooni nende eeldatavatest väärtustest. Kovariantsust kasutades saame mõõta ainult suhte suunda (kas muutujad kipuvad liikuma tandemina või näitavad pöördvõrdelist suhet). Kuid see ei näita seose tugevust ega muutujate sõltuvust.

Teiselt poolt, korrelatsioon mõõdab muutujate seose tugevust. Korraratsioon on kovariantsuse skaleeritud mõõt. See on mõõtmeteta. Teisisõnu on korrelatsioonikordaja alati puhas väärtus ja seda ei mõõdeta ühikutes.

Kahe mõiste suhet saab väljendada järgmise valemi abil:

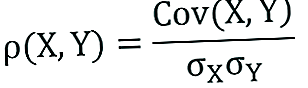
Kus:

• ρ (X, Y) - muutujate X ja Y korrelatsioon
• Cov (X, Y) - muutujate X ja Y kovariantsus
• σ_X - X-muutuja standardhälve
• σ_Y- Y-muutuja standardhälve

Kovariantsuse näide

John on investor. Tema portfell jälgib peamiselt S&P 500 tootlust ja John soovib lisada ABC Corp aktsia. Enne aktsia lisamist oma portfelli soovib ta hinnata aktsia ja S&P 500 suhet.

John ei soovi oma portfelli süsteemitut riski suurendada. Seega pole ta huvitatud portfelli kuuluvate väärtpaberite omamisest, mis kipuvad liikuma samas suunas.

John saab arvutada kovariantsi ABC Corp. ja S&P 500 aktsiate vahel, järgides alltoodud samme:

1. Hankige andmed.

Esiteks saab John nii ABC Corp. aktsia kui ka S&P 500 näitajad. Saadud hinnad on kokku võetud allolevas tabelis:

2. Arvutage iga vara keskmised (keskmised) hinnad.

3. Leidke iga väärtpaberi puhul vahe iga väärtuse ja keskmise hinna vahel.

4. Korrutage eelmises etapis saadud tulemused.

5. Kasutage 4. etapis arvutatud arvu abil kovariantsust.

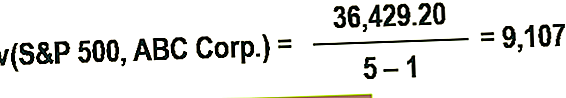
Sellisel juhul näitab positiivne kovariantsus, et aktsia hind ja S&P 500 kipuvad liikuma samas suunas.

Lisaressursid

Finance pakub finantsmodelleerimise ja hindamise analüütikule (FMVA) ™ FMVA® sertifikaati. Liituge 350 600+ üliõpilasega, kes töötavad sellistes ettevõtetes nagu Amazon, JP Morgan ja Ferrari sertifitseerimisprogrammis neile, kes soovivad oma karjääri järgmisele tasemele viia. Õppimise jätkamiseks ja oma karjääri edendamiseks on abiks järgmised finantsvahendid:

• Investeerimine: juhend algajale Investeerimine: juhend algajale Finantsjuhend Investeerimine algajatele õpetab teile investeerimise põhitõdesid ja alustamist. Siit saate teada kauplemise erinevatest strateegiatest ja tehnikatest ning erinevatest finantsturgudest, kuhu saate investeerida.
• Negatiivne korrelatsioon Negatiivne korrelatsioon Negatiivne korrelatsioon on suhe kahe vastassuunas liikuva muutuja vahel. Teisisõnu, kui muutuja A suureneb, muutuja B väheneb. Negatiivset korrelatsiooni tuntakse ka pöördkorrelatsioonina. Vaadake näiteid, diagramme ja
• Risk ja tootlus Risk ja tootlus Investeerimisel on risk ja tootlus omavahel tihedalt seotud. Potentsiaalse investeeringutasuvuse suurenemine käib tavaliselt suurema riskiga käsikäes. Erinevat tüüpi riskide hulka kuuluvad projektipõhine risk, valdkonnapõhine risk, konkurentsirisk, rahvusvaheline risk ja tururisk.
• Riskijuhtimine Riskijuhtimine hõlmab riskitegurite tuvastamist, analüüsimist ja reageerimist neile, mis moodustavad osa ettevõtte elust. Tavaliselt tehakse seda